Расчет расстояний между городами по их координатам

Введение

Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения.

Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.

Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут отличен от постоянного, следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или π*R, где R – радиус сферы.

На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.

Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.

Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.

[править] Введение

Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.

Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут , следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.

большой круг

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.

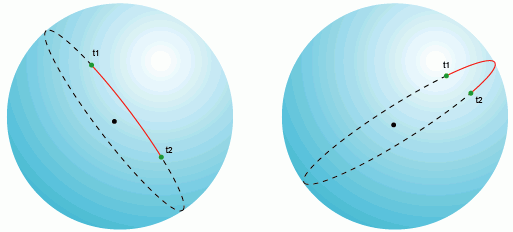расстояние большого круга

На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.

Маршрут Нью-Йорк — Пекин

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.

Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.

Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.

Создание договоров по шаблонам Word в УТ 11.2, БП 3.0 с возможностью хранения в справочнике «Файлы»

Публикация предназначена тем, кто ведет договоры в УТ 11 не только в справочнике «Договоры с контрагентами», но также формирует и согласовывает с контрагентами договоры в формате Word (*.doc). А так как программисты люди ленивые и я не являюсь исключением в этом (хорошем) смысле :), была создана эта печатная форма. Но это не простая печатная форма, а инструмент, который позволяет на основании шаблона, хранящегося в информационной базе в справочнике «Файлы», быстро заполнять и сохранять тут же в справочник «Файлы», но в другую папку, уже заполненный на основании шаблона договор в формате Word.

10 стартмани

Поиск широты и долготы на Яндекс Картах

Рассмотрим, как найти точку на карте по координатам и определить их на Яндекс Картах. Откройте ссылку: https://yandex.ru/maps/?lang=ru/. Поисковая строка веб-карты тоже умеет определять координаты, но здесь их запись немного отличается от Google Maps. Система понимает такой вид: 55.555333,66.666444, где первое значение — широта, второе — долгота. А также более понятную: 45° с. ш. 24° в. д. Как видим, по заданному координату у нас отобразился город Вылча в Румынии.

Поиск по координатам в Яндекс Картах

Чтобы определить долготу и широту точки на Yandex карте, введите название населённого пункта в поисковой строке. После того, как система определит его на карте, вы сможете подсмотреть координаты под названием города слева в блоке. Эти координаты можно добавить в закладки, поделиться ими в других веб-ресурсах или отправить на своё мобильное устройство. Удобная Яндекс Карта слева в информационном блоке предлагает найти популярные заведения: кино, кафе, гостиницы, аптеки и прочее.

Определение координат в Яндекс Картах

В верхнем меню находятся другие инструменты, с помощью которых можно управлять картой или использовать её функции. Можно посмотреть текущую ситуацию на любой дороге мира. Для этого нажмите на кнопку в виде светофора. При помощи кнопки с круговой стрелкой можно отображать панорамирование улиц на карте. Выберите линейку, если необходимо измерить расстояние от одного объекта на карте до другого. Кнопка с бумажным самолётом даёт возможность определить ваше местоположение, а также широту и долготу на спутниковой карте.

Электронная таблица средствами 1С (Версия 2.0)

Функционал электронной таблицы для программ на платформе 1С реализован на основе табличных документов. Функционал реализован в виде обработки. Большую часть формы обработки занимают листы (закладки) с табличными документами, которые выполняет роль электронной таблицы. Листы могут быть добавлены, удалены или переименованы. Ограничение по количеству листов определяется возможностью платформы. В формулах электронной таблицы можно использовать любые языковые конструкции, процедуры и функции 1С, ссылки на другие ячейки электронной таблицы расположенные в том числе и на других листах. Допустимо обращаться к ячейкам электронной таблицы по имени именованной области. В случае использования в формулах электронной таблицы данных из самой таблицы пересчет зависимых ячеек с формулами производится автоматически. Электронную таблицу можно сохранить в файл.

1 стартмани

Алгоритм

Построим алгоритм по общей схеме алгоритмов «разделяй-и-властвуй»: алгоритм оформляем в виде рекурсивной функции, которой передаётся множество точек; эта рекурсивная функция разбивает это множество пополам, вызывает себя рекурсивно от каждой половины, а затем выполняет какие-то операции по объединению ответов. Операция объединения заключается в обнаружении случаев, когда одна точка оптимального решения попала в одну половину, а другая точка — в другую (в этом случае рекурсивные вызовы от каждой из половинок отдельно обнаружить эту пару, конечно, не смогут). Основная сложность, как всегда, заключается в эффективной реализации этой стадии объединения. Если рекурсивной функции передаётся множество из точек, то стадия объединения должна работать не более, чем , тогда асимптотика всего алгоритма будет находиться из уравнения:

Решением этого уравнения, как известно, является .

Итак, перейдём к построению алгоритма. Чтобы в будущем прийти к эффективной реализации стадии объединения, разбивать множество точек на два будем согласно их -координатам: фактически мы проводим некоторую вертикальную прямую, разбивающую множество точек на два подмножества примерно одинаковых размеров. Такое разбиение удобно произвести следующим образом: отсортируем точки стандартно как пары чисел, т.е.:

Тогда возьмём среднюю после сортировки точку (), и все точки до неё и саму отнесём к первой половине, а все точки после неё — ко второй половине:

Теперь, вызвавшись рекурсивно от каждого из множеств и , мы найдём ответы и для каждой из половинок. Возьмём лучший из них: .

Теперь нам надо произвести стадию объединения, т.е. попытаться обнаружить такие пары точек, расстояние между которыми меньше , причём одна точка лежит в , а другая — в . Очевидно, что для этого достаточно рассматривать только те точки, которые отстоят от вертикальной прямой раздела на расстояние, меньшее , т.е. множество рассматриваемых на этой стадии точек равно:

Для каждой точки из множества надо попытаться найти точки, находящиеся к ней ближе, чем . Например, достаточно рассматривать только те точки, координата которых отличается не более чем на . Более того, не имеет смысла рассматривать те точки, у которых -координата больше -координаты текущей точки. Таким образом, для каждой точки определим множество рассматриваемых точек следующим образом:

Если мы отсортируем точки множества по -координате, то находить будет очень легко: это несколько точек подряд до точки .

Итак, в новых обозначениях стадия объединения выглядит следующим образом: построить множество , отсортировать в нём точки по -координате, затем для каждой точки рассмотреть все точки , и каждой пары посчитать расстояние и сравнить с текущим наилучшим расстоянием.

На первый взгляд, это по-прежнему неоптимальный алгоритм: кажется, что размеры множеств будут порядка , и требуемая асимптотика никак не получится. Однако, как это ни удивительно, можно доказать, что размер каждого из множеств есть величина , т.е. не превосходит некоторой малой константы вне зависимости от самих точек. Доказательство этого факта приведено в следующем разделе.

Наконец, обратим внимание на сортировки, которых вышеописанный алгоритм содержит сразу две: сначала сортировка по парам (,), а затем сортировка элементов множества по. На самом деле, от обеих этих сортировок внутри рекурсивной функции можно избавиться (иначе бы мы не достигли оценки для стадии объединения, и общая асимптотика алгоритма получилась бы )

От первой сортировки избавиться легко — достаточно предварительно, до запуска рекурсии, выполнить эту сортировку: ведь внутри рекурсии сами элементы не меняются, поэтому нет никакой необходимости выполнять сортировку заново. Со второй сортировкой чуть сложнее, выполнить её предварительно не получится. Зато, вспомнив сортировку слиянием (merge sort), которая тоже работает по принципу разделяй-и-властвуй, можно просто встроить эту сортировку в нашу рекурсию. Пусть рекурсия, принимая какое-то множество точек (как мы помним, упорядоченное по парам ) возвращает это же множество, но отсортированное уже по координате . Для этого достаточно просто выполнить слияние (за ) двух результатов, возвращённых рекурсивными вызовами. Тем самым получится отсортированное по множество.

Расстояние от точки до точки на плоскости, формула.

Получим формулу для вычисления расстояния между точками и , заданными в прямоугольной декартовой системе координат на плоскости.

Проведем через точки А и В прямые, перпендикулярные координатным осям Ох и Оу. Обозначим проекции точки А на координатные прямые Ох и Оу как и соответственно, а проекции точки В — как и (при необходимости смотрите статью проекция точки на прямую).

В зависимости от расположения точек А и В возможны следующие варианты.

Если точки А и В совпадают, то расстояние между ними равно нулю.

Если точки А и В лежат на прямой, перпендикулярной оси абсцисс, то точки и совпадают, а расстояние равно расстоянию . В предыдущем пункте мы выяснили, что расстояние между двумя точками на координатной прямой равно модулю разности их координат, поэтому, . Следовательно, .

Аналогично, если точки А и В лежат на прямой, перпендикулярной оси ординат, то расстояние от точки А до точки В находится как .

Сейчас будем считать, что точки А и В не совпадают и не лежат на прямой, перпендикулярной координатной оси. Найдем расстояние между ними.

В этом случае треугольник АВС – прямоугольный по построению, причем и . По теореме Пифагора мы можем записать равенство , откуда .

Обобщим все полученные результаты: расстояние от точки до точки на плоскости находится через координаты точек по формуле .

Полученную формулу для нахождения расстояния между точками, можно использовать когда точки А и В совпадают или лежат на прямой, перпендикулярной одной из координатных осей. Действительно, если А и В совпадают, то . Если точки А и В лежат на прямой, перпендикулярной оси Ох, то . Если А и В лежат на прямой, перпендикулярной оси Оу, то .

Видимость объектов – как способ узнать расстояние

По тому различимы объекты, находящиеся вдали глазом или нет, также можно достаточно точно определять расстояние. Тренировкой возможно добиться снижения погрешности в определении длины до 10-20% на 1 км.

Определение расстояния по видимым объектам

Используя этот метод, нужно учитывать, что глаз по-разному воспринимает расстояния:

• в темное время суток расстояние визуально увеличивается;
• при наличии осадков объект будет казаться дальше;
• предмет на равнине кажется ближе, чем на холмистой местности;
• водные преграды сильно скрадывают расстояния;
• темный объект будет казаться дальше, чем светлый.

Данные, приведенные ниже, рассчитаны на определение расстояния до объекта днем в ясную погоду на равнинной местности.

1. Если ваш глаз вдали смог различить деревенский дом, то расстояние до него не более 5 км. Способны рассмотреть трубу на крыше? Это уже 3 км.
2. Если возможно увидеть движение ног человека (идущего или бегущего) – до 700 м.
3. Стволы деревьев, столбы линий связи можно распознать с расстояния не более 1 км.
4. Лицо различимо с расстояния до 100 м.

LКак определить погоду в походных условиях, вы узнаете из статьи: Способы как узнать погоду по приметам на завтра

Формулы

Существует три способа расчета сферического расстояния большого круга.

1. Сферическая теорема косинусов

В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением.

φ1, λ1; φ2, λ2 — широта и долгота двух точек в радианах

Δλ — разница координат по долготе

Δδ — угловая разница

Δδ = arccos {sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ}

Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).

Используется, чтобы избежать проблем с небольшими расстояниями.

3. Модификация для антиподов

Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.

Нахождение расстояния от точки до точки, примеры и решения.

Итак, мы получили формулы для нахождения расстояния между двумя точками координатной прямой, плоскости и трехмерного пространства. Пришло время рассмотреть решения характерных примеров.

Число задач, при решении которых конечным этапом является нахождение расстояния между двумя точками по их координатам, поистине огромно. Полный обзор таких примеров выходит за рамки данной статьи. Здесь мы ограничимся примерами, в которых известны координаты двух точек и требуется вычислить расстояние между ними.

Пример.

На координатной прямой Ох заданы две точки и . Найдите расстояние от начала отсчета до точки А, а также расстояние между точками А и В.

Решение.

Расстояние от начала отсчета до точки А на координатной прямой равно модулю координаты этой точки, поэтому, .

Расстояние между двумя точками равно модулю разности их координат: .

Ответ:

.

Пример.

В прямоугольной декартовой системе координат на плоскости заданы две точки и , где — некоторое действительное число. Найдите все значения , при которых расстояние между точками А и В равно 5 единицам.

Решение.

Расстояние от точки А до точки В по их координатам можно найти по формуле . Подставляем координаты: . С другой стороны по условию . Таким образом, значения находим из уравнения :

Ответ:

расстояние между точками А и В равно 5 при .

Пример.

В трехмерном пространстве заданы координаты двух точек и . Найдите расстояние между ними.

Решение.

Для вычисления расстояния от точки А до точки В по координатам воспользуемся формулой :

Ответ:

расстояние между точками равно девяти.

Список литературы.

• Мордкович А.Г. Алгебра. 7 класс. Часть 1: учебник для учащихся общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.

Некогда разбираться?

Групповая обработка прикрепленных файлов

Кому не знакомы авралы в бухгалтерии, когда налоговая требует представить копии всех документов за два-три года? Кто не получал сюрпризов в виде отсутствия документов, когда завтра их нужно уже представлять проверяющим? 1С предлагает прикрепление и хранение копий документов (в том числе со сканера) в базе, а данная обработка решает вопрос их быстрой подборки, сортировки и выгрузки, а также быстрого и эффективного контроля наличия или отсутствия документов в базе с формированием реестров как выгруженных, так и отсутствующих документов.
В настоящий момент обработка бесплатна, в дальнейшем планируется платная версия с расширенными возможностями.
Скажите решительное «Нет» авралам в бухгалтерии и штрафам за несвоевременное представление документов!

4 стартмани

Внедорожное ориентирование: поиск объекта по азимуту и расстоянию в SAS Планета

SAS Планета – картографическая и навигационная программа, в режиме онлайн доступны спутниковые снимки и карты от Google, Яндекса, Bing и ряда других провайдеров. Работает на ПК и мобильных устройствах на Windows. Очень много функций, но сегодня мы рассмотрим лишь те, которые пригодятся в построении азимутов.

SAS Планета: построение азимута линейкой

Начальная точка. Каким-то образом мы нашли нужный объект на карте, по координатам или проехавшись по виртуальной легенде. Ставим точку в этом месте.

Начальная точка — некий недострой, точные координаты которого нам удалось вычислить.

Начальная точка — некий недострой, точные координаты которого нам удалось вычислить.

От этого объекта нам нужно найти точку по заданному азимуту и расстоянию.

Способ первый – инструмент «Линейка» — начальная точка на недострое, конечная точка в любом другом (или нужном для другого задания) месте. Кроме расстояния сразу отобразится азимут от первой до второй точки.

Построение азимута линейкой.

Построение азимута линейкой.

Чтобы начальная точка попала точно по координатам объекта, достаточно навести мышку на значок точки до появления ее названия. Тогда при постановке точки она окажется точно в основании иконки.

Проекция точки в SAS Планета

Для построения азимутов в SASPlanet есть и специальный инструмент «Проекция точки». Выбираем нужный пункт в меню:

В открывшимся окне вводим нужные данные – расстояние и азимут, а также начальную точку.

Жмем кнопку «Спроецировать», задаем имя метки и все — нужная точка стоит на карте.

Построение азимутов в SAS Планета: геометрический способ («Циркуль»)

Есть и третий способ вычисления азимутов в SASPlanet — геометрический. Для этого нам пригодится еще один инструмент «Циркуль».

Инструмент «Циркуль» открывается в панели инструментов под главным меню программы.

Инструмент «Циркуль» открывается в панели инструментов под главным меню программы.

Первую точку ставим непосредственно на наш недострой, вторую — в любом месте рядом. В открывшемся окне просто вводим нужное значение.

На этом примере мы построили вокруг недостроя окружность диаметром 71 метр.

На этом примере мы построили вокруг недостроя окружность диаметром 71 метр.

Осталось определиться с азимутом.

Расстояние между двумя точками в пространстве

Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (x_a,y_a,z_a), а B имеет координаты (x_b,y_b,z_b) (Рис.5).

AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:

Учитывая, что BM равно разности третьих координат точек B и A, получим:

Из предыдующего параграфа следует, что:

Но AM=A’B’. Тогда из (10) и (11) следует:

Откуда:

Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки \( \small A(x_a; \ y_a ;\ z_a)=A(5;1;0) \) и \( \small B(x_b, \ y_b, \ z_b)=B(-8,-4;21). \) Найти рассояние между этими точками.

Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:

Ответ: .

Расстояние между двумя параллельными прямыми: определение

Определение 1

Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.

Приведем иллюстрацию для наглядности:

На чертеже изображены две параллельные прямые a и b. Точка М1 принадлежит прямой a, из нее опущен перпендикуляр на прямуюb. Полученный отрезок М1Н1 и есть расстояние между двумя параллельными прямыми aиb.

Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.

Теорема

Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.

Доказательство

Пусть нам заданы две параллельные прямые a и b. Зададим на прямой а точки М1 и М2, опустим из них перпендикуляры на прямую b, обозначив их основания соответственно как Н1 и Н2. М1Н1 – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что |М1Н1|=|М2Н2|.

Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: ∠M2M1H2=∠H1H2M1. Прямая М2Н2 перпендикулярна прямой b по построению, и, конечно, перпендикулярна прямой a. Получившиеся треугольники М1Н1Н2 и М2М1Н2 являются прямоугольными и равными друг другу по гипотенузе и острому углу: М1Н2 – общая гипотенуза, ∠M2M1H2=∠H1H2M1. Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: |М1Н1| = |М2Н2|. Теорема доказана.

Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.

Расстояние от точки до прямой − теория, примеры и решения

Рассмотрим эту задачу в двухмерном и трехмерном пространствах.

1. Расстояние от точки до прямой на плоскости

Пусть в двухмерном пространстве задана точка M(x, y) и прямая L:

где q=(m,p) направляющий вектор прямой L.

Найдем расстояние от точки M до прямой (1)(Рис.1).

Алгоритм нахождения расстояния от точки M до прямой L содержит следующие шаги:

• построить прямую L₁, проходящую через точку M и перпендикулярную прямой L,
• найти пересечение прямых L и L₁(точка M₁)
• найти найти расстояние между точками M и M₁.

Уравнение прямой, проходящей через точку M(x, y) имеет следующий вид:

где n=(A,B) нормальный вектор прямой L₁.

Как видно из рисунка Рис.1, для того, чтобы прямая L₁ была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n прямой L₁, поэтому в качестве нормального вектора прямой L₁ достаточно взять направляющий вектор прямой L. Тогда уравнение прямой L₁, представленной уравнением (2) можно записать так:

Откроем скобки

Для нахождения точки пересечения прямых L и L₁, которая и будет проекцией точки M на прямую L, можно решить систему из двух уравнений (1) и (3) с двумя неизвестными x и y. Выражая неизвестную x из одного уравнения и подставляя в другое уравнение получим координаты точки M₁(x₁, y₁).

Найдем точку пересечения прямых L и L₁ другим методом.

Выведем параметрическое уравнение прямой (1):

Подставим значения x и y в (4):

Мы нашли такое значение t=t’, при котором координаты x и y точки на прямой L удовлетворяют уравнению прямой L₁(4). Следовательно, подставляя значение t’ в (5) получим координаты проекции точки M на прямую L:

где x₁=mt’+x’, y₁=pt’+y’.

Далее находим расстояние между точками M и M₁ используя формулу:

Пример 1. Найти расстояние от точки M(−6, 2) до прямой

Решение.

Направляющий вектор прямой (8) имеет вид:

Т.е. m=2, p=−1. Из уравнения прямой (8) видно, что она проходит через точку M’ (x’, y’)=(1, 7)(в этом легко убедится − подставляя эти значения в (8) получим тождество 0=0), т.е. x’=1, y’=7. Подставим значения m, p, x, y, x’, y’ в (6):

Подставляя значение t в (5), получим:

Вычислим расстояние между точками M(-6, 2) и M₁

Упростим и решим:

Ответ:

Расстояние от точки M(-6, 2) до прямой (8) :

2. Расстояние от точки до прямой в пространстве

Пусть в трехмерном пространстве задана точка M(x, y, z) и прямая L:

где q=(m, p, l) направляющий вектор прямой L.

Найдем расстояние от точки M до прямой (9)(Рис.2).

Алгоритм нахождения расстояния от точки до прямой L содержит следующие шаги:

• построить плоскость α, проходящую через точку M и перпендикулярную прямой L,
• найти пересечение плоскости α и прямой L(точка M₁)
• найти расстояние между точками M и M₁.

Уравнение плоскости, проходящей через точку M(x, y, z) имеет следующий вид:

где n=(A,B,C) нормальный вектор плоскости α.

Как видно из рисунка Рис.2, для того, чтобы плоскость α была перпендикулярна прямой L нужно , чтобы направляющий вектор q прямой L была коллинеарна нормальному вектору n плоскости α, поэтому в качестве нормального вектора плоскости α достаточно взять направляющий вектор прямой L. Тогда уравнение плоскости α, представленной уравнением (10) можно записать так:

Откроем скобки

Для нахождения точки пересечения плоскости α и прямой L, которая и будет проекцией точки M на прямую L, выведем параметрическое уравнение прямой (9):

Подставим значения x и y в (11):

Мы нашли такое значение t=t’, при котором координаты x,y и z точки на прямой L удовлетворяют уравнению плоскости (11). Следовательно, подставляя значение t’ в (12) получим координаты проекции точки M на прямую L:

где x₁=mt’+x’, y₁=pt’+y’, z₁=lt’+z’.

Далее вычисляем расстояние между точками M и M₁ используя формулу

которое является расстоянием между точкой M и прямой (9).

Пример 2. Найти расстояние от точки M(1, 2, 1) до прямой

Решение.

Направляющий вектор прямой (15) имеет вид:

Т.е. m=2, p=4, l=−6. Из уравнения прямой (15) видно, что она проходит через точку M’ (x’, y’, z’)=(4, 3, 1)(в этом легко убедится − подставляя эти значения в (15) получим тождество 0=0=0), т.е. x’=4, y’=3, z’=1. Подставим значения m, p, l x, y, z x’, y’, z’ в (13):

Подставляя значение t=t’ в (12), получим координаты точки M₁:

Далее, используя формулу (14) вычисляем расстояние от точки M до прямой (15):

Упростим и решим:

Ответ:

Расстояние от точки M(1, 2, 1) до прямой (15) :

Вычисление расстояния шагами

Умение определять расстояния собственными шагами может пригодиться как для любителей туризма (например, при составлении схем местности и наоборот, при поиске объекта, указанного на карте или плане), так и обычным горожанам, которые занимаются, скажем, спортивной ходьбой.

Длина шага — величина постоянная

Шаги используют в качестве мерной единицы по причине того, что человек обычно делает одинаковые по длине шаги, когда идет размеренным шагом по ровной поверхности. Именно эту длину своего шага рекомендуется вычислить и запомнить, как эталонную.

На изменение эталонной длины влияет:

• усталость человека,
• температура воздуха, в жару шаги короче и скорость движения меньше,
• движение по пересеченной местности,
• ходьба в группе, когда мы интуитивно или намеренно подстраиваемся под скорость и шаг других людей,
• тяжелый рюкзак.

Способ «Мокрые ноги

1. Способ «Мокрые ноги»

   Смысл такого измерения в том, что нужно «наследить» мокрыми ногами, затем взять рулетку и узнать расстояние от одной пятки до другой. Для чистоты расчетов, следует сделать несколько шагов, померить расстояния и вычислить среднее значение.

   Для метода подойдет любая лужа, если рядом есть сухой асфальт, можно пройти по снегу, грязи, песчаному пляжу, специально намочить ноги и прогуляться дома по полу. Главное, чтобы оставались следы от ступни.

2. Способ ходьбы на короткое расстояние Отмерьте на ровной поверхности рулеткой расстояние 10 метров. После этого пройдите и посчитайте количество шагов. Разделите 10 метров на шаги, получите длину одного шага. Затем пройдите в обратную сторону, и снова высчитайте длину шага. Вычислите среднее значение шага.
3. По карте Для данного метода подойдет карта, схема местности с объектами А и Б, находящимися в относительной близости друг от друга и расстояние между которыми легко вычислить. Идите из точки А к точке Б и считайте шаги. Разделите расстояние по полученное количество – узнаете длину собственного шага. Вместо бумажной карты можно использовать навигатор, проложив маршрут между двумя точками и затем пройдя его.
4. По росту Зная рост, также можно высчитать длину шага, однако вычисление будет слишком усредненным. Для этого рост, выраженный в сантиметрах, нужно умножить на 0,413 (для женщин) или 0,415 (для мужчин).

Имея длину шага, теперь можно без труда считать расстояния в походе или на прогулке. Интересно, что если ввести такой подсчет в привычку, то скоро вы заметите, что считаете шаги уже по инерции. Есть два способа учитывать шаги.

1. Считать каждый шаг.
2. Считать через шаг, т.е. только правую ногу или только левую. Это более удобный вариант для длительных переходов.

Каким прокладываются маршруты в Яндекс Карты

Динамические карты, разработанные компанией Yandex, являются универсальным инструментом. Они способны отобразить любую точку на земле с поразительной точностью. Водители и пешеходы могут строить в них маршруты с любой протяжённостью. А также выбирать готовые маршруты (кратчайший, самый простой и т.д.). Или перемещаться между несколькими выбранными точками. Сервис показывает пробки на дорогах, погодные условия и места для парковки.

Прокладка маршрута Яндекс Карты

Яндекс Карты доступны на разных устройствах и для разных систем: Windows, Mac, Android, iOS, Linux и пр. Загруженные карты в мобильных устройствах могут работать без интернета. Для использования карт Москвы оффлайн, их нужно предварительно загрузить. Скачиваются файлы как по странам, так и по городам. Файл карты столицы России весит около 280 Мб. Карты можно настраивать вручную.

Яндекс Карты показывают ДТП в реальном времени

При этом пользователи могут обсуждать дорожные события в приложении. С их помощью некоторые новости обновляются онлайн. У вас есть возможность написать отзыв о тех или иных придорожных заведениях и сервисах. А также изменить уже существующую информацию в базе данных онлайн карт.

Расстояние между точками в пространстве, формула.

Введем прямоугольную систему координат Оxyz в пространстве. Получим формулу для нахождения расстояния от точки до точки .

В общем случае, точки А и В не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки А и В плоскости, перпендикулярные координатным осям Ох, Оу и Oz. Точки пересечения этих плоскостей с координатными осями дадут нам проекции точек А и В на эти оси. Обозначим проекции .

Искомое расстояние между точками А и В представляет собой диагональ прямоугольного параллелепипеда, изображенного на рисунке. По построению, измерения этого параллелепипеда равны и . В курсе геометрии средней школы было доказано, что квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений, поэтому, . Опираясь на информацию первого раздела этой статьи, мы можем записать следующие равенства , следовательно,
откуда получаем формулу для нахождения расстояния между точками в пространстве .

Эта формула также справедлива, если точки А и В

• совпадают;
• принадлежат одной из координатных осей или прямой, параллельной одной из координатных осей;
• принадлежат одной из координатных плоскостей или плоскости, параллельной одной из координатных плоскостей.

Советуем ознакомиться

Как делать ножи из картона. как сделать нож из бумаги. какие материалы потребуются Штормовка Двухствольные ружья (вертикальное и горизонтальное): обзор, характеристики, производители Географические координаты якутска (широта и долгота) Весенние грибы Сколько дней человек сможет прожить без еды и воды